statistics

In case of multicollinearity, there are columns (variables) in the data set, that are identical or linearly dependent. That happens, when columns are the exact multiple of another column. Our standard assumption of a \(\small{ N\times K }\) matrix is that \(\small{ rk\left(X\right)=K }\). However, when there is perfect multicollinearity, the rank of \(\small{ X }\) will be smaller than \(\small{ K }\).

In practice, perfect multicollinearity is quite rare. More often, we observe features that are nearly linearly dependent. That is called nearly perfect multicollinearity.

The problem of multicollinearity is that \(\small{ X^\prime X }\) is not regular (=singular) anymore. A singular matrix cannot be inverted. There is no solution for \(\small{ \left(X^\prime X\right)^{-1} }\) and hence, the OLS estimator \(\small{ \hat{\beta}={\left(X^\prime X\right)^{-1}\ X}^\prime y }\) is not identifiable.

A typical mistake, often seen among beginners, is the dummy trap. That is encoding a discrete variable with \(\small{ k }\) levels as \(\small{ k }\) individual dummy variables. There is always the case, that one level can be calculated by the other levels. Thus, the correct way of encoding is using \(\small{ k-1 }\) dummy variables.

Example: Correlation between Age and Years_since_schooling

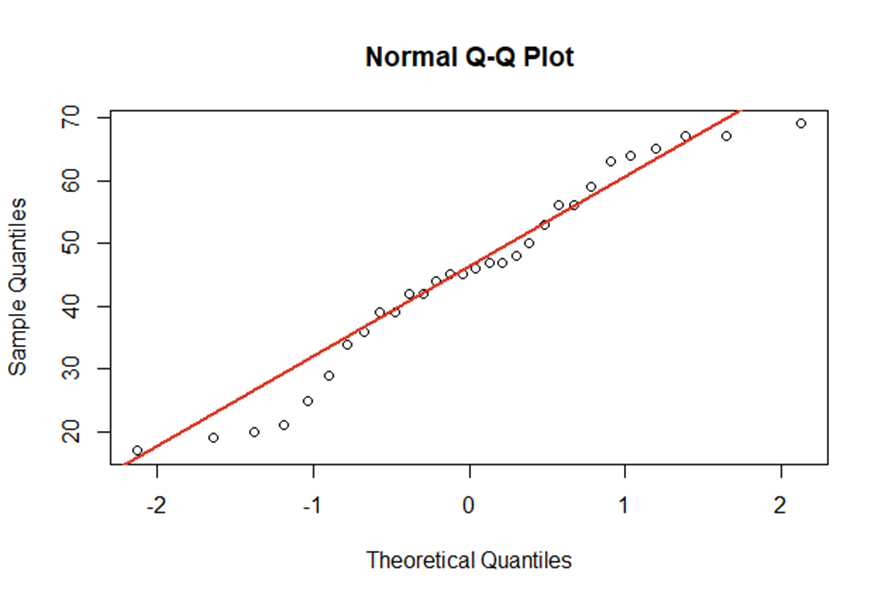
Multicollinearity can be identified by checking the correlation matrix of \(\small{ X }\) . The following example shows a high correlation between the age of a person and the years since graduation at school. Here, the result is quite intuitive.

A strong correlation hints that the regressors are nearly perfect multicollinear. In result, the coefficients in regression analysis will not show high significance. They will be unstable and imprecise. Furthermore, we’d expect a high standard error rate. In some cases even numerical errors will arise by calculating the OLS regression.
Even though the coefficients are unstable and insignificant, the fitted values will be almost unchanged in many cases. The problem of nearly perfect multicollinearity hence lies in an improper understanding of the coefficients. The interpretation of the model will be extremely difficult.

Measurement for Multicollinearity

We already saw that the correlation between two variables can give us a hint about the presence of multicollinearity. Another common approach for identifying multicollinearity is the measurement of the variance inflation factor.

We define an auxiliary regression
\[{\hat{\beta}}_i=\left(x_i^\prime Q_{-i}x_i\right)^{-1}x_i^\prime Q_{-i}y\]
where \(\small{ Q_{-i}=I-P_{-i}=X_{-i}\left(X_{-i}^\prime X_{-i}\right)^{-1}X_{-i}^\prime }\) is the residual maker without the \(\small{ i }\)-th column \(\small{ x_i }\).

The coefficient of determination is hence
\[R_i^2=1-\frac{RSS_i}{S_{x_ix_i}}\]
where \(\small{ S_{x_ix_i} }\) is the variance of the \(\small{ i }\)-th column.

The variance inflation factor is now denoted as
\[VIF_i=\frac{1}{1-R_i^2} \]
As a rule of thumb, we’d expect no problem if \(\small{ VIF_i\le5 }\), but in case of \(\small{ VIF_i>10 }\) there seems to be serious multicollinearity. Then there are various possible options how to treat multicollinearity. The simplest way is ignoring it completely in those cases when the predictions are still valid and there seems to be no bad influence. If that is impossible, then one of the linear dependent variables can be omitted or transformed.

Very often in order to come closer to the “true” model, regression models contain non-linear terms. In 1969 James Ramsey developed the Regression Equation Specification Error Test (RESET) as a general specification test. It examines whether non-linear combinations of the fitted values explain the target variable.

Linear Model:

\[H_0:\ \mathbb{E}\left[y_i\middle|\ x_i\right]=x_i\beta\]

Non-Linear Model:
\[H_1:\ \mathbb{E}\left[y_i\middle|\ x_i\right]\neq x_i\beta\]

The procedure of testing is described hereafter:

1. Build the standard OLS linear regression model.
2. Use the fitted values of the linear regression and add them to a new model. Set \(\small{ K }\) (often \(\small{ K=1,2,3 }\) )
   \[{\hat{y}}_{RESET}=x_i\beta+\sum_{k=1}^{K}\omega_k\ {\hat{y}}^{k+1}\]
3. Use the common F-test to decide if \(\small{ {H_0:\ \omega}_{1..K}=0 }\).
4. If \(\small{ H_0 }\) is rejected, the linear model is misspecified and hence there are non-linear terms.
   In R, the test can be run by the command \(\small{ resettest(model) }\).

When applying OLS regression or related statistics (e.g. F-test), there are certain assumptions that are essential for a robust and unbiased model. The normality assumption is one of them. We expect the error terms to be normally distributed. In many cases, outlying data points are the reason for non-normality.
There are many graphical ways to identify non-normality with plots. For instance, QQ-plots show the empirical quantiles vs. the theoretical quantiles of a normal distribution. The better our empirical data points fit the red line, the closer is our data to a normal distribution.

As already shown, visualisations are perfect for getting a first overview of the data. However, you should also consider test statistics with \(\small{ H_0:\ \varepsilon_i\sim N }\) and \(\small{ H_1: \varepsilon_i\sim D_0\neq\ N }\).
Two important test statistics are the Kolmogorov-Smirnow test and the Jarque-Bera test.

Tests for Heteroscedasticity

For basing inference on OLS, the error terms need to be homoscedastic. That is a constant variance of the error terms. Again, we can apply graphical methods in order to get a first overview. Therefore, we plot the studentised residuals vs. the fitted values and examine the distribution of the data points. If there is an increase in variance, there might be heteroscedasticity.

White Test

The White test for heteroscedasticity has the following hypotheses:

\[H_0:\ \mathbb{E}\left[\varepsilon_i^2\middle|\ X_i\right]=\sigma^2=const\]
\[H_1:\ \mathbb{E}\left[\varepsilon_i^2\middle|\ X_i\right]=\sigma_i^2\neq\sigma_{k\neq i}^2\neq const\]

The null hypothesis assumes that the error terms all have the same constant variance. The alternative hypothesis on the contrary assumes that there are differences between the variances of the error terms and they are hence not constant.
With a regression model \(\small{ \hat{y}=X\hat{\beta} }\), the White test procedures as follows:

1. Extract the residuals \(\small{ {\hat{\varepsilon}}_i }\) and square them: \(\small{ {\hat{\varepsilon}}_i^2 }\)
2. Run auxiliary regression \(\small{ {\hat{\varepsilon}}_i=\beta_0+\beta_1x_1+\ldots+\beta_nx_n }\).
   Idea: If there is heteroscedasticity, then \(\small{ \mathbb{E}\left[\varepsilon_i^2\middle|\ x_i\right] }\) depends on \(\small{ x_i }\) and thus \(\small{ x_i }\) influences \(\small{ \varepsilon_i^2 }\).
3. Let \(\small{ N }\) be the number of observations and \(\small{ R_{aux}^2 }\) the R-Squared of the auxiliary regression model.
4. Calculate the test statistic \(\small{ \theta=N\ast\ R_{aux}^2 }\) and test whether \(\small{ \theta }\) follows the \(\small{ \mathcal{X}_q^2 }\)-distribution with \(\small{ q }\) degrees of freedom or not.
   \(\small{ H_0:\theta\sim\mathcal{X}_q^2 }\) or \(\small{ H_1:\theta\sim\mathcal{D}\neq\mathcal{X}_q^2 }\)

R-Code: Manual White Test for Heteroscedasticity

# Extract Squared Residuals
res=lr$residuals
res2=res^2

# Run Auxiliary Regression
aux=lm(res2~df$X)

# Calculate Test Statistic
N=length(res)
R2=summary(aux)$r.squared
theta= N*R2

# Testing Result
p_value <- 1 - pchisq(theta, N-1) 
if(p_value>0.05){
  print("Homoscedasticity, accept H0!")
}
else{
  print("Heteroscedasticity, reject H0!")
}

Conclusion

If we detect heteroscedasticity, the Gauss-Markow assumptions are violated. Hence, we cannot apply OLS regression, but have to use FGLS instead:

Whenever building a regression model, we have certain assumptions (e.g. Gauss-Markow theorem). For instance, a normal distribution of the error terms is essential for OLS regression. We use model diagnostic statistics or graphs in order to detect problems or errors in our modelling.

Residual Analysis

In a regression model, we call the difference between the fitted values and the observed target values the residuals.

\[e=\hat{y}-y=X\hat{\beta}-y=\left(I-P\right)y\]

\[= My \sim \left(0,\ \sigma^2\left(I-P\right)\right)\]

where \(\small{M=I-P}\) is the residual maker and \(\small{P=X\left(X^\prime X\right)^{-1}X^\prime}\) is the projection (“hat”) matrix.
A residual analysis can help us to identify outliers, check for linearity, normality, homoscedasticity or time series properties. For checking, we transform the residuals in a standardised form. The most important transformation was established by Student:

Studentised Residuals

\[t=\frac{e}{\hat{\sigma}\sqrt{1-p_{ii}}}\]

where \(\small{p_{ii} }\) is the \(\small{ i }\) -th diagonal element in the hat matrix and \(\small{ \hat{\sigma} }\) is an appropriate estimate of the variance.
There are two options to calculate the variance of the residuals. The internal studentisation estimates the residual variance based on all observations:
\[{\hat{\sigma}}^2\ =\frac{e^\prime e}{N-K}=\frac{1}{N-K}\sum e_j^2\]

However, if the \(\small{ i }\) -th case is suspected to have a high leverage effect and hence might be an outlier, the external studentisation excluded the \(\small{ i }\) -th observation in order to calculate the variance only based on the other observations.
\[{\hat{\sigma}}_{-i}^2\ =\frac{{(e}_{-i})^{\prime} e_{-i}}{N-K-1}=\frac{1}{N-K}\sum e_{j\neq i}^2\]

By plotting the studentised residuals against the fitted values, the occurrence of heteroscedasticity can be graphically seen. Moreover, hints for normal distribution and linearity are visible.
Let’s take a look at an example. The following plot shows the studentised residuals of a linear model’s prediction of the blood pressure based on the age of a person. The plot looks distorted and we discover a data point far away from the other observations. We can suspect this data point to be a potential outlier. The red line shows the studentised regression line and should be located at approximately \(\small{ y=0 }\) and the data points closely above and below.

In the second plot, I have removed the outlying data point and now, the regression line perfectly fits the x-axis ( \(\small{ y=0 }\) ). Furthermore, the data points are randomly located above and over the red curve, which is a sign for linearity. There might be an increase in the variance of the studentised residuals as the fitted values increase. This could be a hint for heteroscedasticity and more tests need to be applied.

The R code for this visualisation is as follows:

# Delete Outlier
df.new=df[-2,]

# Train Linear Model
lr.new=lm(Blood_Pressure ~., data=df.new)

# Visualise with ggplot2
ggplot(lr.new, aes(x=lr.new$fitted.values,y=rstudent(lr.new))) 
   + geom_point(color="black") 
   + geom_smooth(method='lm', se=F, color="#d83c2d") 
   + ggtitle("Studentised Residuals vs. Fitted Values (without outlier) ")
   + xlab("Fitted Values") + ylab("Studentised Residuals")

Formal Tests for Outliers

After considering outlier detection by visualisation of the data, we now want to identify outliers by formal statistical measurements.

The Leverage Effect

The leverage effect of a data point is given by \(\small{ 0\le\ pii\le1 }\) , which is the \(\small{ i }\)-th diagonal element of the hat matix. In R the \(\small{p_{ii} }\) can be calculated by the function \(\small{ hatvalues(model) }\) . The higher the value of the leverage, the higher will be the effect of this observation on the regression coefficients. First conclusions can therefore be drawn by identifying data points with higher leverage compared to the other observations. As a rule of thumb, in cases of \(\small{ p_{ii}>\frac{2K}{N} }\) the data points need further examination.

The Mahalanobis Distance

An important numerical method to detect outliers is the squared Mahalanobis distance. It considers the depending or surrounding variables in context and measures the distance between the j-th observation and the center of the distribution.
\[D^2\ =\ \left(x_j\ -\ \mu\right)^\prime\ \mathrm{\Sigma}^{-1}\left(x_j\ -\ \mu\right)\]
with the covariance matrix \(\small{ \mathrm{\Sigma} }\).

The Cook’s Distance

The Cook’s distance answers the question, how much influence is caused by the \(\small{i }\)-th data point in our regression model.

\[C_i=\frac{\left(\hat{y}-{\hat{y}}_{-i}\right)^2}{K{\hat{\sigma}}^2}=\frac{\varepsilon_i^2}{K{\hat{\sigma}}^2}\ast\left[\frac{p_{ii}}{1-p_{ii}}\right]\]

where \(\small{ {\hat{\sigma}}^2\ =\frac{e^\prime e}{N-K}=\frac{1}{N-K}\sum e_j^2 }\) . As a rule of thumb, the \(\small{ i }\)-th data point has a large influence if \(\small{ C_i>\frac{4}{N} }\).

We define a criterion \(\small{ C(m) }\) that measures the quality of a model \(\small{ m }\) . In general, we need to find the model \(\small{ m^{*} }\) that minimises the selection criterion \(\small{ C(m) }\) for all possible \(\small{ m }\) .
For beginning, let us recall the mean squared prediction error ( \(\small{ MSPE }\) ) for our model \(\small{ m }\) . The MSPE is the expected value of the squared difference between the fitted values (prediction) \(\small{ {\hat{y}}_{i}\left(m\right) }\) and the values of the unobservable function \(\small{ y_i^\ast }\) .

\[MSPE(m)=\frac{1}{N} \sum_{i=1}^N E[(\hat{y}_i (m)-y_i)^2]\]

The MSPE contains information about the model bias, the estimation error and the variance. With an increasing number of included features \(\small{ \left|m\right| }\) , the model bias will decrease and the estimation error increase. An estimation of the \(\small{ MSPE }\) can be given by

\[\widehat{MSPE}\left(m\right)=\frac{1}{N}RSS\left(m\right)+2\frac{\left|m\right|}{N}{\hat{\sigma}}^2\]

where \(\small{ RSS=N\ast\ MSE=\sum\nolimits_{i=1}^{N}\left({\hat{y}}_i\left(m\right)-y_i\right)^2 }\) . The increasing number of variables \(\small{ \left|m\right| }\) is used as a “punishment” or penalty. As the number of included features grows, the higher will be the value of the selection criterion and hence this model is not being preferred. This prevents overfitting. Collin Mallows later proposed a normalised version of this criterion:

\[C_p\left(m\right)=\frac{RSS\left(m\right)}{{\hat{\sigma}}^2}-N+2\left|m\right|\]

Both criteria lead to the same optimal model \(\small{ m }\) .

Cross Validation Criteria

Alternatives to the MSPE are cross-validation criteria:

\[CV(m)=\frac{1}{N}\sum_{i=1}^{N}\left({\hat{y}}_{-i}(m)-y_i\right)^2\]

This criterion is the mean squared difference between the true value \(\small{ y_i }\) and the prediction \(\small{ {\hat{y}}_{-i}\left(m\right) }\) trained on a data set without the \(\small{ i }\) -th point. Thus, it is called a leave-one-out estimator.

Generalised Information Criterion

An important measure of model selection is the generalised information criterion ( \(\small{ GIC }\) ).

\[GIC\left(m\right)=\ln{\left({\widetilde{\sigma}}^2\left(m\right)\right)}+a_N\frac{\left|m\right|}{N}\]

The \(\small{ GIC }\) is based on the logarithm of the maximum-likelihood estimator \(\small{ {\widetilde{\sigma}}^2\left(m\right) }\) .

We can derive two special cases of the \(\small{ GIC }\) that are very popular among statisticians.

1. Akaike Information Criterion (AIC)

The Akaike Information Criterion sets \(\small{ a_N=2 }\) in the \(\small{ GIC }\) formula. Thus, we have

\[AIC\left(m\right)=\ln{\left({\widetilde{\sigma}}^2\left(m\right)\right)}+2\frac{\left|m\right|}{N}\]

When using OLS regression, the maximum likelihood estimator for the variance of a model’s residuals distributions is \(\small{ {\widetilde{\sigma}}^2\left(m\right)=RSS/N }\) , where \(\small{ RSS }\) is the residual sum of squares.

\[AIC_{OLS}\left(m\right)=\ln{\left(\frac{RSS}{N}\right)}+2\frac{\left|m\right|}{N}\]

The \(\small{ AIC }\) criterion is asymptotically optimal under certain conditions. As well, as \(\small{ CV }\) , \(\small{ Cp }\) and \(\small{ MSPE }\) . However, \(\small{ AIC }\) is not consistent. Under the assumption that the “true model” is not in the candidate set, we are interested in the unknown “oracle model” \(\small{ m^\ast }\) . As \(\small{ N\rightarrow\infty }\) ,

\[\frac{\left|\left|g-\hat{y}\left(\hat{m}\right)\right|\right|^2}{\left|\left|g-\hat{y}\left(m^\ast\right)\right|\right|^2} \rightarrow m_{true}\]

Moreover, the \(\small{ AIC }\) is asymptotically equivalent to the leave-one-out \(\small{ CV }\) criterion.

2. Baysian-Schwarz Information Criterion (BIC)

The Akaike Information Criterion sets \(\small{ a_N=\ln(N) }\) in the \(\small{ GIC }\) formula. Thus, we have

\[BIC\left(m\right)=\ln{\left({\widetilde{\sigma}}^2\left(m\right)\right)}+\ln(N)\frac{\left|m\right|}{N}\]

Again, when using OLS regression, the maximum likelihood estimate for the variance of a model’s residuals distributions is \(\small{ {\widetilde{\sigma}}^2\left(m\right)=RSS/N }\) , where \(\small{ RSS }\) is the residual sum of squares.

\[BIC_{OLS}\left(m\right)=\ln{\left(\frac{RSS}{N}\right)}+\ln(N)\frac{\left|m\right|}{N}\]

The BIC Criterion is consistent. However, it is not asymptotically optimal. As \(\small{ N\rightarrow\infty }\) ,
\[\hat{m} \rightarrow m_{true}\]

In Econometrics and Data Science, a necessary procedure in building a prediction model is validation. I already presented the most common techniques of model validation in this article.
Let us now have a deeper look on these methods from statistical perspective. For robust prediction models it is vital to split the data with \(\small{ N }\) observations into two different sets. The train set with \(\small{ n_1<N }\) rows and the test/validation set with \(\small{ n_2=N-n_1 }\) rows.
Now, we build the regression model with the training data. Using the mean-square-error, we afterwards evaluate the regression model based on the untouched test data.
\[MSE=\frac{1}{n_2}\sum_{i=n_1+1}^{N}\left({\hat{y}}_i-y_i\right)^2\]
We choose the model that minimises the MSE for our validation set.

I have also described the procedure of feature selection from a data scientist’s perspective in this aricle.

Sequential Variable Selection

There are basically four different algorithms or procedures for selecting variables to include in the model.

Forward Selection

Starting from a minimum set of variables based on economic theory, the algorithm determines which regressor (not yet included) reduces most the RSS in the regression model. The algorithm iteratively adds variables until a stopping criterion is met. That is when \(\small{\Delta RSS < \tau }\), where \(\small{ \tau }\) is a threshold metric to avoid adding variables with little or no reduction of RSS.

Backward Elimination

The other way around, the algorithm starts with the whole set of variables and iteratively excludes features that add little or no reduction of RSS to the model.

Stepwise Selection

The combination of forward and backward selection. The algorithm can add and exclude variables at each iteration.

Random variable selection

Often neglected in traditional statistic theory, but nowadays becoming very popular in famous machine learning algorithms, a random selection of variables can provide a proper prediction model. Though this method is only used in combination with many different individual random models in a composite ensemble model.

Frisch-Waugh Theorem

Assume that we have a regression model with \(\small{ k }\) different variables. In some cases, we might not be interested in all \(\small{ k }\) variables, but in a subset only.
\[y=X\beta+Z\gamma+\varepsilon\]

The theorem uses a projection matrix \(\small{ P=Z^\prime\left(Z^\prime Z\right)^{-1}Z^\prime }\) so that \(\small{ Q=\left(I-P\right)}\). Now, \(\small{ Q }\) is the orthogonal projection onto the column space of \(\small{ Z }\) and therefore eliminates the influence of \(\small{ Z }\).

\[y=X\beta+Z\gamma+\varepsilon \\ \Leftrightarrow\ X^\prime Qy =X^\prime QX\beta+X^\prime QZ\gamma \\ \Leftrightarrow\ X^\prime Qy =\ X^\prime QX\beta \\ \Leftrightarrow\hat{\beta} =\left(X^\prime Q\ X\right)^{-1}\ X^\prime Qy\]

After this transformation, we have our model \(\small{ Qy=QX\beta+Q\varepsilon }\) with the variance \(\small{ \mathbb{V}\left(\hat{\beta}\right)=\sigma^2\left(X^\prime Q\ X\right)^{-1} }\) .
The vectors of the OLS residuals \(\small{ \varepsilon_0=y-(X\hat{\beta}+Z\hat{\gamma}) }\) and \(\small{ \varepsilon_{FW}=Qy-QX\hat{\beta} }\) coincide.

By eliminating \(\small{ Z }\) with Frisch-Waugh, we still capture the effect of \(\small{ Z }\) but without including the additional variables in our model.

Model Misspecification

We call a model misspecified if we discover over- or underspecification. Let’s have a quick look at the difference:

The F-test provides a test statistic to identify model misspecification. Let there be two different regression models \(\small{ m0_{N\times K}:\ y=X\beta+\varepsilon }\) and \(\small{ m1_{N\times L}:\ y=X\beta+Z\omega+\varepsilon }\). We assume that \(\small{ m1 }\) is the true model and formulate the hypotheses
\[H_0:\ \omega=0\] or \[H_1:\ \omega\neq0\]

We now calculate the F-statistic, with \(\small{ N-K-L }\) degrees of freedom, where \(\small{ N }\) is the number of rows, and \(\small{ K+L }\) denote the number of columns.
\[F\left(m\right)=\frac{(RSS\left(m0\right)-RSS\left(m1\right))/L}{RSS(m1)/(N-K-L)\ \ }\]

The null hypothesis \(\small{ H0 }\) is rejected at level of significance \(\small{ \alpha }\) , if \(\small{ F\left(m\right)>F_{L,\ \ \ \left[N-K-L\right]}^{1-\alpha} }\) holds.

Bias: Correlation and Underspecification

Let’s assume that two regressors \(\small{ \beta_1 }\) and \(\small{ \omega_0 }\) are positively correlated in our model
\[y_i=\beta_0+\beta_1x_i+\omega_0z_i+\varepsilon_i\]
If we now build our regression model without \(\small{ \omega_0 }\) , then \(\small{ {\hat{\beta}}_1 }\) will measure the effect of \(\small{ \omega_0 }\) on \(\small{ y_i }\) and will not be unbiased.

\[Bias\left({\hat{\beta}}_1\right)=\mathbb{E}\left[{\hat{\beta}}_1\right]-\beta_1=\frac{corr(x,z)}{Var(x)}\omega_0\]
If both regressors are positively correlated (and \(\small{ \omega_0>0 }\) ), we expect a positive bias.