
Financial Derivatives: An In-Depth Analysis
Financial derivatives are financial instruments whose value is derived from the performance of an underlying asset. These assets can include stocks, bonds, commodities, currencies, indices, and futures contracts. Derivatives are used for various purposes, including hedging risks, speculating on future price movements, and gaining exposure to specific asset classes. This article provides a comprehensive overview of financial derivatives, focusing on the main categories and their respective features.
Structured Products and Certificates
Structured products, also known as certificates, are debt securities linked to an underlying asset. Investors do not directly purchase the asset but instead participate in its performance through the certificate. The issuer of the certificate is obligated to deliver the promised return based on the performance of the underlying asset at maturity. Certificates can be designed with a fixed maturity or as open-end products, which have no specified maturity date.
Certificates can exhibit various risk profiles, depending on their structure. They offer risk-averse investors opportunities for downside protection, while more aggressive investors can pursue higher potential returns through leveraged products. The creditworthiness of the issuer plays a crucial role in the certificate’s overall risk profile.
Categories of Certificates
Bonus Certificates: These products offer a 1:1 participation in the underlying asset’s performance. If the asset’s price does not breach a pre-defined threshold, the investor receives a bonus. If the threshold is breached, the bonus is forfeited. These certificates are suitable for investors who expect stable asset prices.
Discount Certificates: These certificates allow investors to purchase the underlying asset at a discounted price. However, the profit potential is capped at a predetermined level. They are suitable for investors anticipating modest price movements in the asset.
Guarantee Certificates: These products provide a guaranteed minimum return at maturity. In exchange for this protection, investors only participate in a portion of the asset’s gains. They are suitable for investors seeking capital preservation and some exposure to price increases.
Leverage Certificates: These products offer investors the opportunity to participate disproportionately in the performance of the underlying asset using leverage. The potential for both gains and losses is magnified, and the total investment can be lost if a specified knock-out threshold is crossed. Bull certificates target strongly rising prices, while bear certificates target sharply falling prices.
Index Certificates: These products offer a 1:1 participation in the performance of an index. A pre-determined ratio determines the issuance price, allowing investors to participate in the index’s performance with smaller investment amounts. They are suitable for investors expecting a rise in the index’s value.
Risks Associated with Certificates
Certificates can carry varying degrees of risk depending on their structure. Some certificates serve as hedging instruments, while others are designed for speculation. Some key risks associated with certificates include:
- Issuer risk: Investors must trust the issuer to fulfill its obligations at maturity. This risk is related to the issuer’s creditworthiness.
- Market price risk: Investors must consider the typical price risks associated with securities.
- Underlying asset delivery risk: Some certificates may require the delivery of the underlying asset at maturity, which carries additional risks.
- (Total) loss risk: Particularly speculative certificates can result in substantial losses, even total loss, if the underlying asset performs poorly.
Options
Options are conditional derivatives that give the buyer the right, but not the obligation, to buy (call) or sell (put) an underlying asset at a specified price (strike price) on or before a specified date. The seller (writer) of the option has the obligation to fulfill the contract if the buyer exercises the option. In exchange for this right, the buyer pays a premium to the option seller.
Options can be traded on exchanges such as EUREX or over-the-counter (OTC) markets. They are commonly used for hedging, speculation, and income generation strategies.
Types of Options
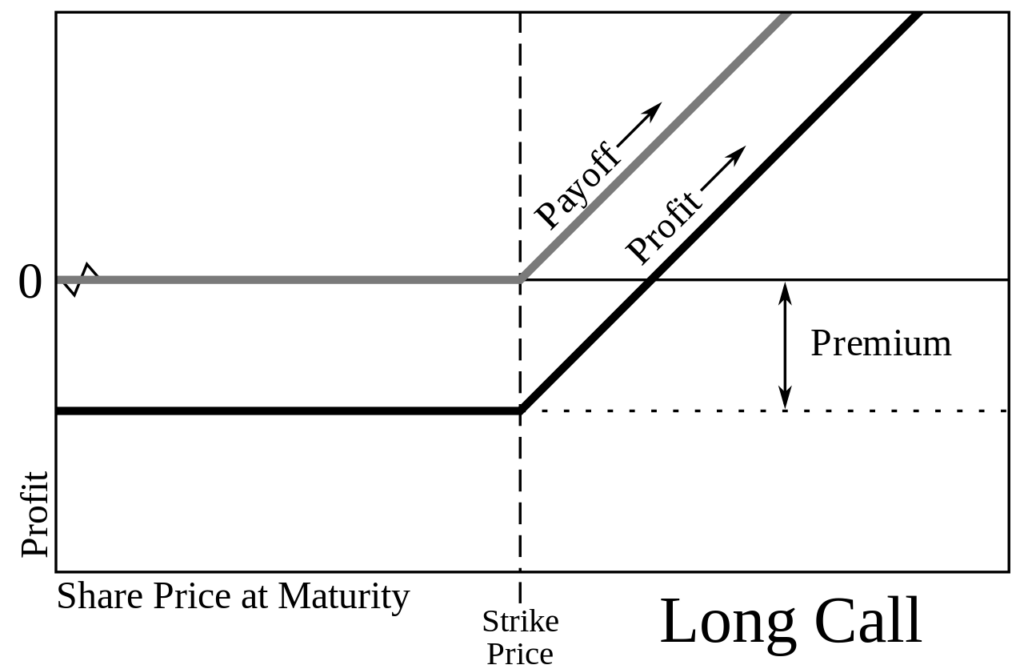
Call Options: A call option gives the buyer (holder) the right to purchase an underlying asset at the strike price. A long call position offers the holder the right to buy the asset, while a short call position obligates the writer to deliver the asset if the option is exercised.
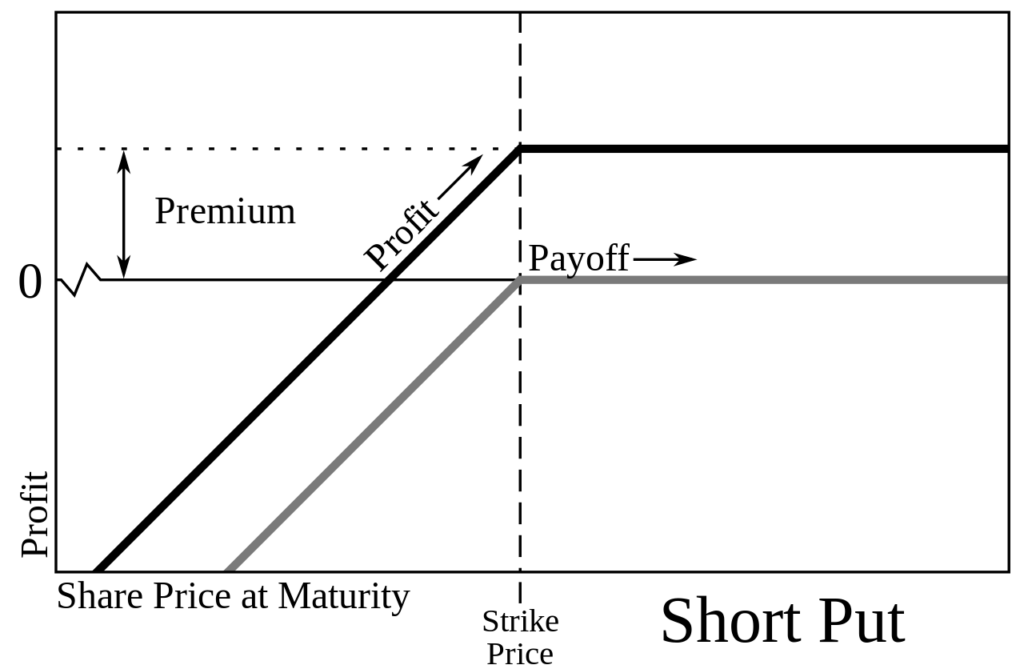
Put Options: A put option gives the holder the right to sell an underlying asset at the strike price. A long put position offers the holder the right to sell the asset, while a short put position obligates the writer to purchase the asset if the option is exercised.
Profit and Loss Profiles of Options
The profit and loss potential for each option position depends on the underlying asset’s price movement and the option’s premium.
- Long Call: Unlimited profit potential with increasing asset prices; limited loss to the premium paid.
- Short Call: Limited profit to the premium received; unlimited loss potential with increasing asset prices.
- Long Put: Limited profit potential with decreasing asset prices; limited loss to the premium paid.
- Short Put: Limited profit to the premium received; substantial loss potential with decreasing asset prices.


Put-Call Parity
Put-call parity is a financial principle that establishes a relationship between the prices of European call and put options. It ensures a balance between the two types of options, helping to determine the option’s value.
Call + Present Value of Strike Price = Put + Spot Price of Underlying Asset
This equation states that the value of a call option plus the present value of the strike price, discounted at the risk-free interest rate, should be equal to the value of a put option plus the current spot price of the underlying asset.
To understand the put-call parity principle more clearly, consider the positions of long call and long put holders:
Long Call: When an investor holds a long call position, they pay a call premium for the right to buy the underlying asset at the strike price. If the investor chooses to exercise this right, they need to pay the strike price to acquire the asset. In the put-call parity equation, this payment is represented as the present value of the strike price. This is the amount of money that, when invested at the risk-free interest rate, would grow to the strike price by the option’s expiration date.
Long Put: When an investor holds a long put position, they pay a put premium for the right to sell the underlying asset at the strike price. If the investor chooses to exercise this right, they need to deliver the underlying asset, which they already possess in their portfolio. The value of this asset is represented as the spot price of the underlying asset in the put-call parity equation.
The put-call parity principle is essential for maintaining a no-arbitrage condition in the options market. If the parity equation does not hold, it creates an arbitrage opportunity, where traders can exploit the price difference between the call and put options to generate risk-free profits. In an efficient market, arbitrageurs will quickly act on such opportunities, causing option prices to adjust and restoring the put-call parity.
Option Risk Parameters (Greeks)
Options are influenced by various factors, such as price changes in the underlying asset, changes in implied volatility, interest rate changes, and time decay. The Greeks are sensitivity measures used to quantify the impact of these factors on option prices.
- Delta (Δ): Measures the change in the option’s value for a one-unit change in the underlying asset’s price.
- Vega (V): Measures the change in the option’s value for a 1% change in implied volatility.
- Theta (Θ): Measures the change in the option’s value for a one-day decrease in time to expiration.
- Rho (ρ): Measures the change in the option’s value for a 1% change in interest rates.
- Gamma (Γ): Measures the change in delta for a one-unit change in the underlying asset’s price.
